単回帰分析 with Python

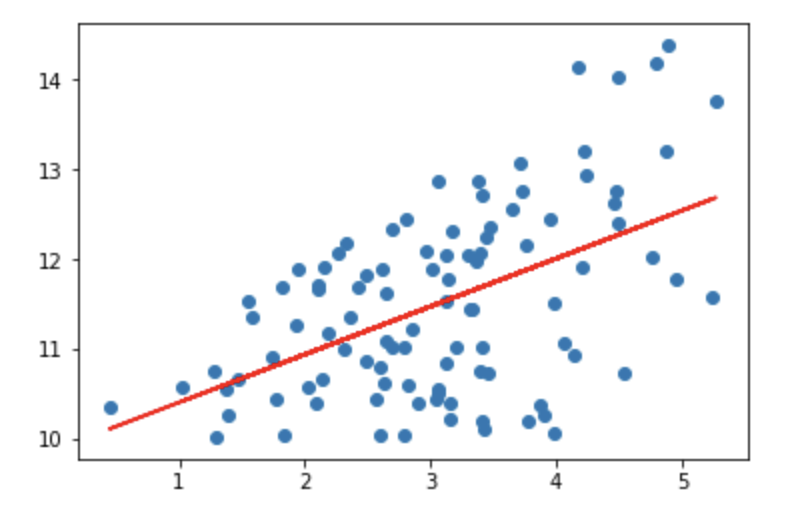
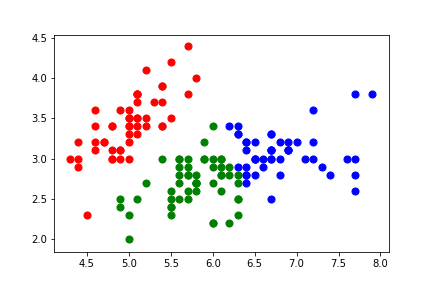
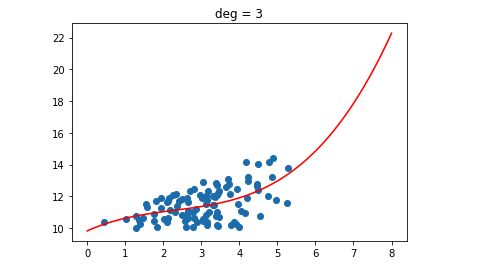
単回帰分析とは

回帰係数が１つで独立変数が１つ
下の式で表せる回帰を単回帰という。

$$ y = \beta_0 + \beta_1 x$$

中学校でやった１次関数の形です。

Pythonで単回帰分析

stats.linregress(x, y)で単回帰

線形単回帰は、stats.linregress(x, y)を使います。
scipyから、statsをインポートします。
このメソッドを通すと、

1. 傾き
2. 切片
3. 相関係数
4. P値(t検定で使う)
5. 推定勾配の標準誤差

の順で値が返ってきます。
Standard error of the estimated gradient.を直訳しただけなので、この推定勾配の標準誤差はなんのことかわかりません。飛ばします。

ソースコード

import numpy as np
from pylab import *
from scipy import stats

#ランダムな数を固定
np.random.seed(0)
x = np.random.normal(3.0, 1.0, 100)
y = 10 + x * np.random.rand(100)

#散布図
sc = scatter(x, y)
plt.show(sc)

'''
単回帰
'''

slope, intercept, r_value, p_value, std_err = \
stats.linregress(x, y)

print("傾き：{0}\n切片：{1}\n相関係数：{2}\nP値：{3}\n\
標準誤差：{4}".format(slope,intercept, r_value, p_value,std_err))

#直線を描く
fitline  = slope * x + intercept
plt.scatter(x, y)
plt.plot(x, fitline, c='r')
plt.show()

出力結果

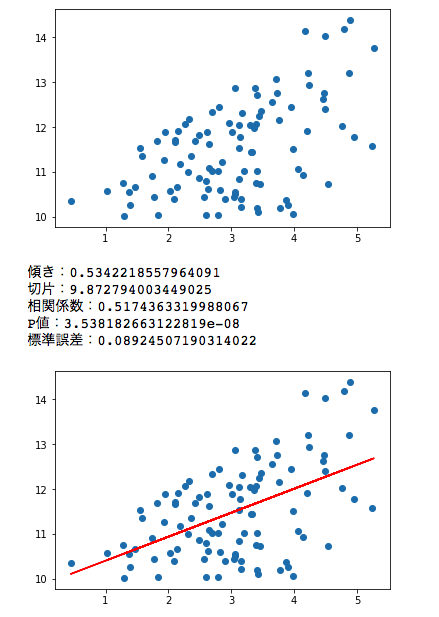
sklearnのLinearRegressionで単回帰

sklearnのLinearRegressionで単回帰を実行します。

LinearRegressionの場合は、P値は算出されません。

ソースコード

import numpy as np
import matplotlib.pyplot as plt
 
#ランダムな数を固定
np.random.seed(0)
x = np.random.normal(3.0, 1.0, 100)
y = 10 + x * np.random.rand(100)

x = x.reshape(-1, 1)
y = y.reshape(-1, 1)


#回帰係数を計算
from sklearn.linear_model import LinearRegression

lr = LinearRegression().fit(x, y)

slope = lr.coef_
intercept = lr.intercept_

#直線を描く
fitline  = slope * x + intercept
plt.scatter(x, y)
plt.plot(x, fitline, c='r')
plt.show()

出力