SIR,SEIR|感染症流行過程の数理モデル

SIR,SEIR|感染症流行過程の数理モデ
SIRモデル
1. Pythonによる実装
SEIRモデル
1. Pythonによる実装
参考

SIR,SEIR|感染症流行過程の数理モデ

SIRモデル

感染症の短期的な流行過程を決定論的に記述するモデル方程式
$$
\frac{dS(t)}{dt} = -\beta S(t) I(t)
\\
\frac{dI(t)}{dt} = \beta S(t) I(t) – \gamma I(t)
\\
\frac{dR(t)}{dt} = \gamma I(t)
$$
閉鎖的な(人の移動がない)集団を3つの状態に分けます．

S: 免疫のない感染する可能性のある集団
I: 感染している人
R: 感染後に回復した人/死亡した人

パラメータなど

$\beta$: 感染率
$\gamma$: 回復率や隔離率
$\beta I(t)$: 時間tにおける感染力

Pythonによる実装

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
 
N = 1_000_000
D = 14
R0 = 2
 
#initial_state
I_0 = 1
R_0 = 0
S_0 = N - I_0 - R_0
 
#params
gamma = 1/D
beta = R0 * gamma
 
#time
times =np.arange(0,366, 1)
 
var_0 = [S_0, I_0, R_0]
 
def SIR(var, t, N, beta, gamma):
    dSdt = - beta*var[0]*var[1]/N
    dIdt = beta*var[0]*var[1]/N-gamma*var[1]
    dRdt = gamma*var[1]
     
    return [dSdt, dIdt, dRdt]
 
result = odeint(SIR, var_0, times, args=(beta, gamma))
 
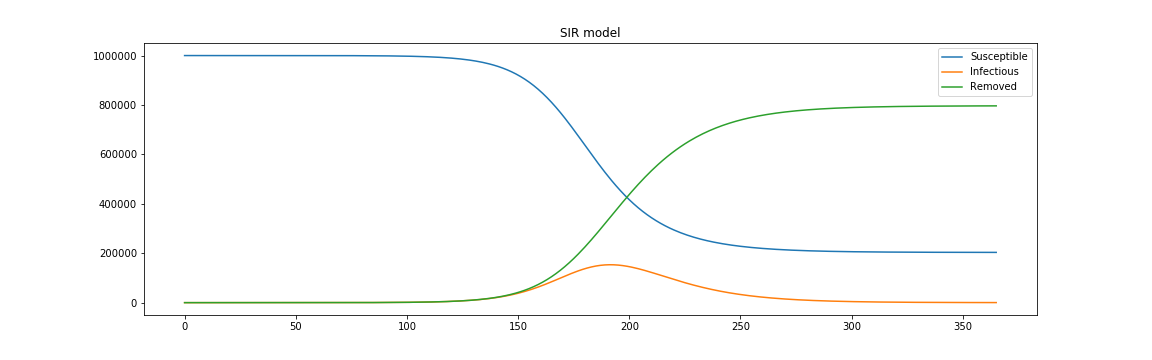
plt.figure(figsize=(16, 5))
plt.plot(times,result)
plt.legend(['Susceptible','Infectious', 'Removed'])
plt.show()

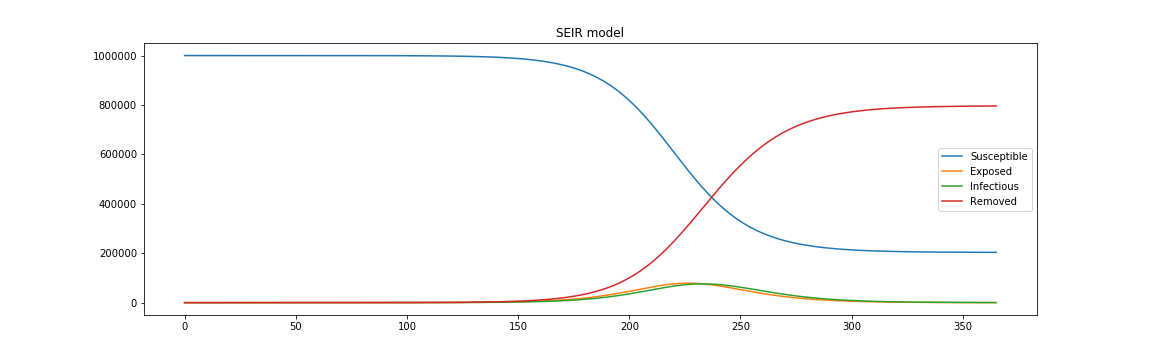
SEIRモデル

$$
\frac{dS(t)}{dt} = -\beta S(t) I(t)
\\
\frac{dE(t)}{dt} = \beta S(t) I(t) – \epsilon E(t)
\\
\frac{dI(t)}{dt} = \epsilon E(t) – \gamma I(t)
\\
\frac{dR(t)}{dt} = \gamma I(t)
$$
閉鎖的な(人の移動がない)集団を4つの状態に分けます．

S: 免疫のない感染する可能性のある集団
E: 感染->発症していない人
I: 感染->発症した人
R: 感染後に回復した人/死亡した人

$\beta$: 感染率
$\gamma$: 回復率や隔離率
$\epsilon ^{-1}$: 感染待ち時間
潜伏期間

Pythonによる実装

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
 
N = 1_000_000
L = 7
D = 7
R0 = 2
 
#initial_state
E_0 = 1
I_0 = 0
R_0 = 0
S_0 = N - E_0 - I_0 - R_0
 
#params
gamma = 1/D
epsilon = 1/L
 
beta = R0 * epsilon / N
 
#time
times =np.arange(0,366, 1)
 
var_0 = [S_0, E_0, I_0, R_0]
 
def SEIR(var, t, beta, epsilon, gamma):
    dSdt = -beta * var[0] * var[2]
    dEdt = beta * var[0] * var[2] - epsilon * var[1]
    dIdt = epsilon * var[1] - gamma * var[2]
    dRdt = gamma * var[2]
     
    return [dSdt, dEdt, dIdt, dRdt]
 
result = odeint(SEIR, var_0, times, args=(beta, epsilon, gamma))
 
plt.figure(figsize=(16, 5))
plt.plot(times,result)
plt.legend(['Susceptible', 'Exposed', 'Infectious', 'Removed'])
plt.show()

SIR,SEIR|感染症流行過程の数理モデ

SIRモデル

Pythonによる実装

SEIRモデル

Pythonによる実装

参考