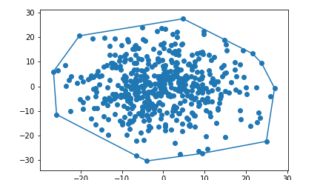
シグモイド関数は、ロジット関数の逆関数
ロジット関数
$$
logit ( p ) = \log \left( \frac { p } { 1 – p } \right)
$$
シグモイド関数
$$
y = \frac { 1 } { 1 + e ^ { – p } }
$$
シグモイド関数の逆関数を計算する
$$
\begin{array} { c } {y = \log \frac { p } { ( 1 – P ) }} \\
e ^ { y } = \frac { p } { 1 – p } \\
( 1 – p ) e ^ { y } = p \\
e ^ { y } – p e ^ { y } = p \\
e ^ { y } = p \left( 1 + e ^ { y } \right) \\
p = \frac { e ^ { g } } { 1 + e ^ { y } } \\
p = \frac { e ^ { y } \cdot e ^ { – y } } { \left( 1 + e ^ { y } \right) e ^ { – y } } \\
p = \frac { 1 } { 1 + e ^ { – y } } \\
\end{array}
$$
変数を入れ替える
$$
y = \frac { 1 } { 1 + e ^ { – p } }
$$