K-Means:Pythonでクラスタリング

K-means法

N個のデータをランダムにK個のクラスタに振り分ける。
それぞれのクラスタのセントロイド(重心) \(\mu_k\ (k=1,…K)\)を求める。

$$
q_{ik} =
\begin{cases}
1 &\ &k=argmin_i \|x_i – \mu_i\|^2 \\
0 &\ &other \\
\end{cases}
$$

評価関数
$$
J(q_{ik}, \mu_k) = \sum^{N}_{i=1}\sum^{K}_{k=1}q_{ik}\|x_i – \mu_k \|^2 \\
\frac{\partial J(q_{ik}, \mu_k)}{\partial \mu_k} = 2 \sum^{N}_{i=1}q_{ik}(x_i – \mu_k) = 0 \\
\mu_k = \frac{\sum^{N}_{i=1}q_{ik}x_i}{\sum^{N}_{i=1}q_{ik}}
$$

sklearnでkmeans

アヤメのデータセットを使います。

今回は、散布図を使って図示していきたいので、２変数しか使用しません。
“sepal length”と”sepal width”のみを使用します。
(PCAなどで次元削減してもいいのかも)

プログラム

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

from sklearn.cluster import KMeans

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target

demo_X = X[:,:2]

kmeans = KMeans(n_clusters = 3, init = 'k-means++', random_state = 1)
y_kmeans = kmeans.fit_predict(demo_X)

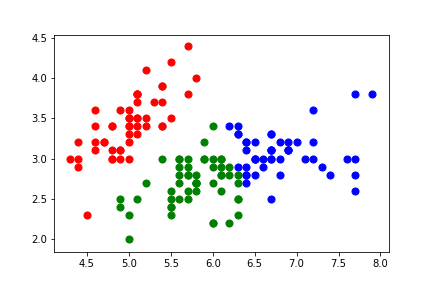
plt.scatter(demo_X[y_kmeans == 0, 0], demo_X[y_kmeans == 0, 1], s = 50, c = 'red')
plt.scatter(demo_X[y_kmeans == 1, 0], demo_X[y_kmeans == 1, 1], s = 50, c = 'blue')
plt.scatter(demo_X[y_kmeans == 2, 0], demo_X[y_kmeans == 2, 1], s = 50, c = 'green')
plt.savefig('iris_kmeans_cluster.png')
plt.show()

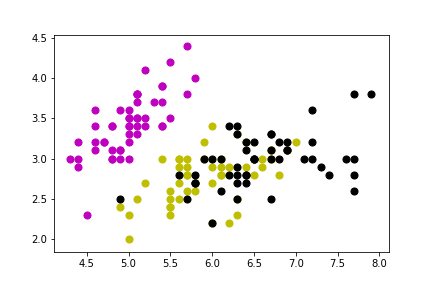
plt.scatter(demo_X[y == 0, 0], X[y == 0, 1], s = 50, c = 'm')
plt.scatter(demo_X[y == 1, 0], X[y == 1, 1], s = 50, c = 'y')
plt.scatter(demo_X[y == 2, 0], X[y == 2, 1], s = 50, c = 'k')
plt.savefig('iris_kmeans_true.png')
plt.show()

データ数が多い場合のMiniBatchKMeans

データが多い場合は、MiniBatchKMeansを使います。

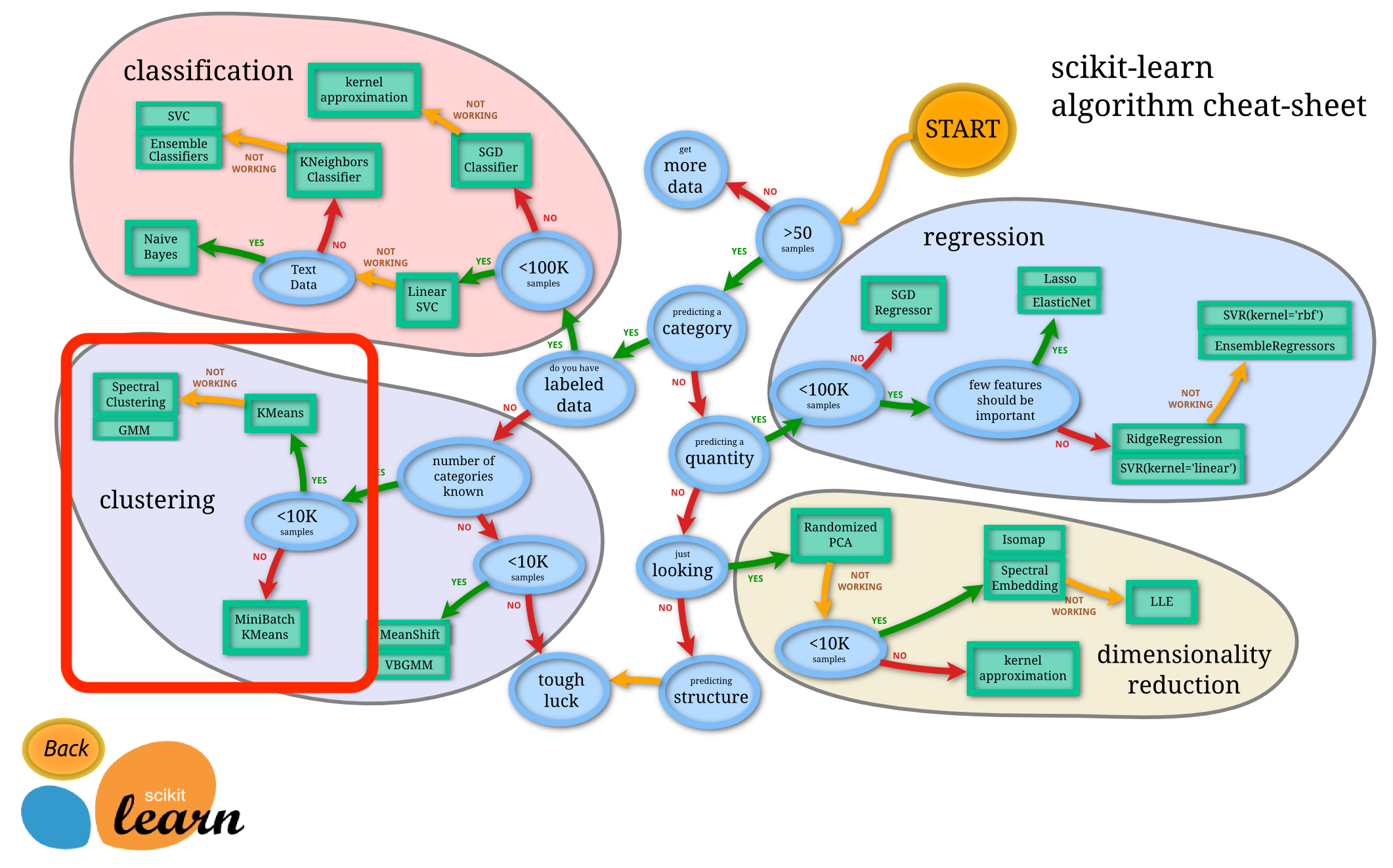
引用:https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html

scikit-learnのチートシートでは、10kを超えるデータにおいては、MiniBatchKMeansになっています。

from sklearn.cluster import MiniBatchKMeans as MBKMeans

#MiniBatchKMeans(n_clusters=8, init='k-means++', max_iter=100, batch_size=100, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init=3, reassignment_ratio=0.01)

mbkmeans = MBKMeans(n_clusters, batch_size)
red = mbkmeans.fit_predict(X)

メモ

k-means algolism
step1:choose the number K of cluster

step2:select at random K points.
the centroids(not necessarily from your datset)

step3:Assign each data point to the closest centroid
that forms K clusters

step4:Compute and place the new centroid of each cluster

step5:Reassign each data point to the new closest centroid.
If any reassignment took place, go to step4 ,otherwise go to FIN

参考