主成分回帰（PCR）Python

主成分回帰：PCR

主成分回帰（Principal Component Regression）は、PCRと略されます。

ここでは、PCRと呼ぶことにします。

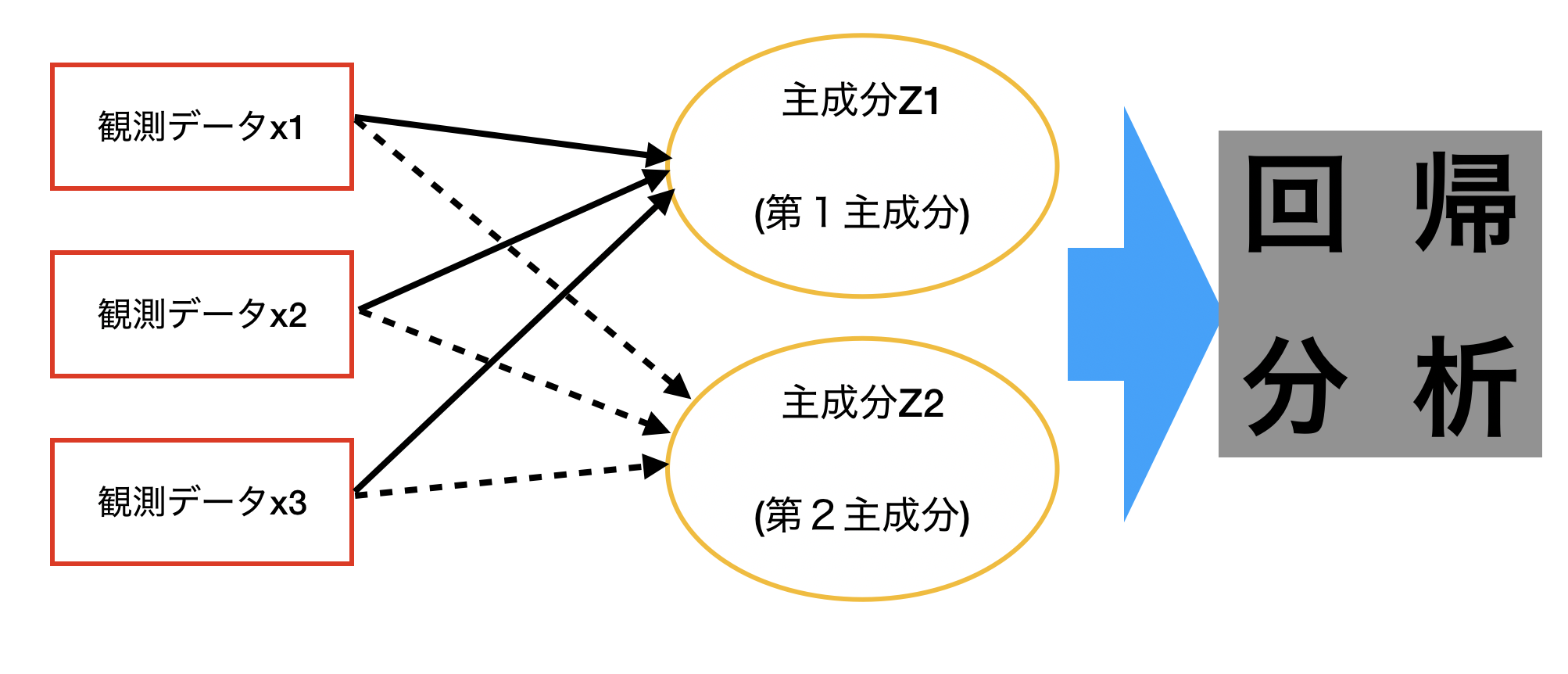
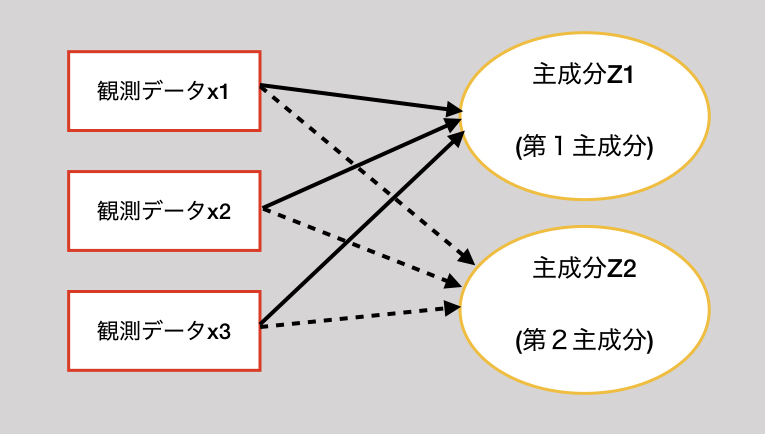
説明変数のデータXを主成分分析（PCA)を行って、主成分を得えます。

PCAは、主成分の分散が最大になるように主成分を抽出します。

この主成分を説明変数とし、最小二乗法によって重回帰分析を行う。

主成分分析（ここでは、PCAと呼ぶことにする）と、重回帰分析を組み合わせたものが、主成分回帰（PCR）である。

主成分分析を利用して、少数の線型独立な変数（主成分）を簡単に作成することができる。

多重共線性の問題なく実行できます。

PythonでPCR

データの前処理とか、データの種類は気にしないで実装します。
(カテゴリとか数値とかバラバラです。）
とりあえず、標準化だけしています。

多分これが、PCRだと思います。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
 
boston = load_boston()
train_X, val_X, train_y, val_y = train_test_split(boston.data, boston.target, test_size=0.3, random_state=0)
 
#PCA
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
std.fit(train_X)
 
std_train_X = std.transform(train_X)
std_val_X = std.transform(val_X)
 
from sklearn.decomposition import PCA
 
pca = PCA(n_components=5)
 
pca.fit(std_train_X)
 
pca_train_X = pca.transform(std_train_X)
pca_val_X = pca.transform(std_val_X)

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

#回帰分析
lr = LinearRegression()
lr.fit(pca_train_X, train_y)

pred_y = lr.predict(pca_val_X)

#平均2乗誤差
mean_squared_error(pred_y, val_y)

参考

https://datachemeng.com/wp-content/uploads/2017/06/partialleastsauares.pdf