多重比較の問題
検定回数を増やすと、検定全体としての第1種の誤り(Type I error)が起こる確率が高くなる問題。
FWER(FamilyWise Error Rate)は、検定全体で少なくとも1回はType Ⅰ errorが起こる確率のこと。
有意水準\(\alpha\)の下で、検定をn回繰り返した時のFWERは以下のようになっている。
$$
FWER = 1 – (1 – \alpha)^n
$$
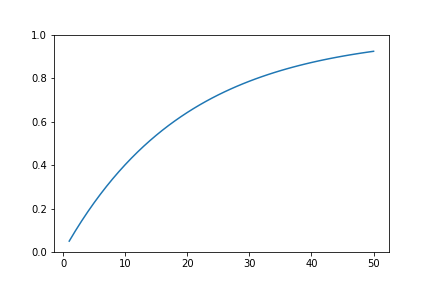
下の図から分かるように、検定回数を増やすと、FWERが高くなる。
例えば、\(\alpha=0.05 n=50\)では、FWERが0.92となる。
ほぼ、Type Ⅰ errorが起こっていると考えられる。
2種類の誤り
第1種の誤り(Type Ⅰ error)
第1種の誤り(Type Ⅰ error)とは、実際には、\(H_0\)が正しいにも関わらず、\(H_0\)を棄却してしまう誤り
Type Ⅰ errorの確率は、\(\alpha\)で表される。
第2種の誤り(TypeⅡerror)
第2種の誤り(TypeⅡerror)とは、実際には、\(H_0\)が誤っているにも関わらず、\(H_0\)を採択してしまう誤り
Type Ⅱ errorの確率は、\( 1 – \beta\)で表される。
\(\beta\)は、\(H_0\)を棄却する確率で、検出力である。
FWER (Family Wise Error Rate)による制御
p値に基づいた、Bonferroni法は、保守的で厳しい補正手法として知られる。
統計量に基づいた方法
- Fisher’s LSD
- Tukey’s HSD
- Dunnet
p値に基づいた方法
- Bonferroni法
- Holm法
FDR (False Discovery Rate)による制御
- Benjamini-Hochberg法