特異値分解
$$
\Large
M = U \Sigma V ^ { * }
$$
\(U\):m次ユニタリ行列
左特異行列と
随伴行列が逆行列となる行列で、固有値の絶対値、特異値、行列式の絶対値が1となる。
\(\sum{}\):\(m\)行\(n\)列行列
特異値行列
\(\sum{}\):対角成分が特異値の\(m\)行\(n\)列行列
\(\sigma_p\)は、特異値です。
m=nの場合は、下のような対角行列になります。
$$
\sum{} =
\left( \begin{array} { c c c c } { \sigma _ { 1 } } & { } & { } & { 0 } \\ { } & { \sigma _ { 2 } } & { } & { } \\ { } & { } & { \ddots } & { } \\ { 0 } & { } & { } & { \sigma _ { p } } \end{array} \right)
$$
それ以外は次のような場合分けになります。
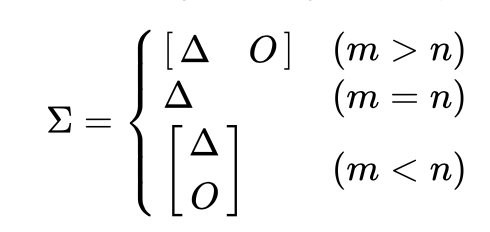
\(V\):n次随伴行列
右特異行列
ユニタリ行列の転置行列かつ、複素共役をとった行列
Pythonで特異値分解
Pythonで特異値分解するにはnumpyのlinalg.svd()を使用する。
import numpy as np np.linalg.svd()
プログラム
import numpy as np
A = np.array([[1,2],[3,4]])
#特異値分解
U, s, V = np.linalg.svd(A, full_matrices=True)
s = np.diag(s)
#確認
print("U = \n", U)
print("s = \n", s)
print("V = \n", V)
#A = UsV
UsV = np.dot(np.dot(U, s), V)
print("A = \n", A)
print("UsV = \n", UsV)
結果
\(A = UsV\)となっていることが確認できる。