Pythonで統計-平均-中央値-最頻値-分散-標準偏差
今回勉強したこと。
- 平均:np.mean(データ)
- 中央値:np.median(データ)
- 最頻値:stats.mode(データ)
- 分散:np.var(データ)
- 標準偏差:np.std(データ)
平均
np.random.normalは、平均値mean、標準偏差SDの正規分布から、ランダムにn個の値を格納します。
import numpy as np
#正規分布(mean, SD:standard deviation, n)
incomes = np.random.normal(27000, 15000, 10000)
#平均を求める
means = np.mean(incomes)
print('平均値:{0}' .format(means))
中央値
中央値は、ソートしたデータの真ん中の値です。
import numpy as np
#正規分布(mean, SD:standard deviation, n)
incomes = np.random.normal(27000, 15000, 10000)
#中央値
median = np.median(incomes)
print("中央値:{0}".format(median))
最頻値
最頻値は、最も頻繁に出てくる値のことです。
np.random.randint()は、コメントを見てください。
from scipy import stats
import numpy as np
#18から90まで500個のランダム整数
ages = np.random.randint(18, high=90, size=500)
stats =stats.mode(ages)
print("最頻値:{0}".format(stats))
#result -> 最頻値、度数の順で表示される
分散
import numpy as np
#正規分布(mean, SD:standard deviation, n)
incomes = np.random.normal(27000, 15000, 10000)
var = incomes.var()
#var = np.var(incomes)でも可能
print("分散:{}".format(var))
標準偏差
import numpy as np
#正規分布(mean, SD:standard deviation, n)
incomes = np.random.normal(27000, 15000, 10000)
sd = incomes.std()
#sd = np.std(incomes)でも可能
print("標準偏差:{0}".format(sd))
分散と標準偏差
分散は、標準偏差の2乗(平方)です。
または、標準偏差は、分散の2乗根(平方根)です。
import numpy as np
#正規分布(mean, SD:standard deviation, n)
incomes = np.random.normal(27000, 15000, 10000)
#SD V
sd = incomes.std()
var = incomes.var()
sd1 = var**(1/2)
var1 = sd**2
print("標準偏差:{0}\n分散から求めた標準偏差:{1}".format(sd,sd1))
print("分散:{0}\n標準偏差から求めた分散:{1}".format(var,var1))
共分散と相関係数
共分散
$$S_{xy} = \frac{1}{n}\sum{(x_i – \bar{x})(y_i – \bar{y})}$$
相関係数
$$r_{xy} = \frac{S_{xy}}{S_x S_y}$$
共分散-np.cov(x,y)-
共分散np.cov(x,y)について、
\begin{pmatrix} S_{xx} & S_{xy} \\ S_{yx} & S_{yy} \end{pmatrix}
といった感じに行列として出力されます。
今回、2変数なので右上と、左下の値が共分散です。
左上は、xの分散
右下は、yの分散になります。
ソースコード
import numpy as np
np.random.seed()
x = np.random.normal(3.0, 1.0, 1000)
y = np.random.normal(10.0, 4.0, 1000)
#共分散
covs = np.cov(x, y)
print("xの分散:{0}\nyの分散:{1}\n\
共分散:{2}\n".format(np.var(x),np.var(y),covs))
出力結果
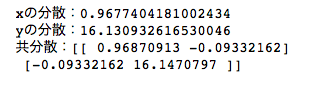
共分散は、分散行列として出力されてますね。
左上は、xの分散・右下は、yの分散になっていることが確認できます。
右上と左下は、同じ値になっていることが確認できます。
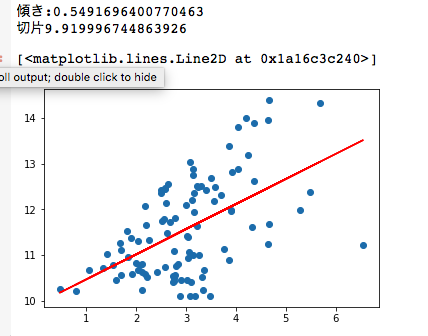
相関係数-np.corrcoef(x, y)-
相関係数np.corrcoef(x, y)についても、分散と同様に
\begin{pmatrix} r_{xx} & r_{xy} \\ r_{yx} & r_{yy} \end{pmatrix}
といった感じに行列として出力されます。
ソースコード
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
x = np.random.normal(3.0, 1.0, 1000)
y = np.random.normal(10.0, 4.0, 1000)
#相関係数
cor = np.corrcoef(x, y)
print("相関係数:{0}".format(cor))
#散布図
plt.show(scatter(x, y))
出力結果
![]()
相関係数も、行列として出力されてますね。
対角成分が同じになっていることが確認できます。
右上と左下がxとyの相関係数になっています。
参考