VIF統計量をPythonで計算

VIF統計量をPythonで計算
使うデータ
statsmodelライブラリを使う
ライブラリを使わない
1. ソースコード
参考

VIF統計量をPythonで計算

pythonでvifを計算していきます。

pythonでvifを計算するには、ライブラリを使う方法があります。

vifについては、多重共線性とVIF統計量の求め方にも書いたので合わせて参照ください。

使うデータ

データは、bostonデータを使います。

load_boston()

statsmodelライブラリを使う

statsmodelライブラリを使います。
インポートするものを下に示します。

from statsmodels.stats.outliers_influence import variance_inflation_factor

データを用意する

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

#データをインポート
from sklearn.datasets import load_boston

#statsmodelsのvifをインポート
from statsmodels.stats.outliers_influence import variance_inflation_factor


# サンプルデータを用意
dataset = load_boston()

# 標本データを取得
data_x = pd.DataFrame(dataset.data,columns=dataset.feature_names)

# 正解データを取得
data_y = pd.DataFrame(dataset.target,columns=['target'])

statsmodelsでvifを計算する

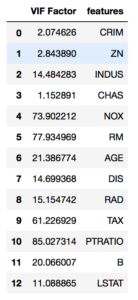
#vifを計算する
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(data_x.values, i) for i in range(data_x.shape[1])]
vif["features"] = data_x.columns

#vifを計算結果を出力する
print(vif)

#vifをグラフ化する
plt.plot(vif["VIF Factor"])

結果

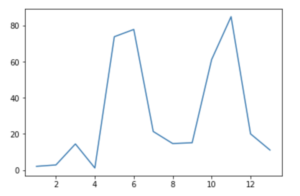
ライブラリを使わない

こちらは、前回の多重共線性とVIF統計量の求め方と同じ計算方法でvifを計算しました。

vif統計量は、以下の通り78通りあります。

$$\begin{eqnarray}{}_{13} \mathrm{ C }_2 = 78 \end{eqnarray}$$

VIFが10以上になるものであれば、多重共線性が存在している可能性があるので対処しなければならない。

結果は、省略します。

ソースコード

for t in range(data_x.shape[1] - 1):
    s = t
    for i in range(data_x.shape[1] - 1 - s):
        #変数１　変数２　vif　の順に表示される
        print(s+1, s + 1 + i + 1, 1 / (1 - np.corrcoef(data_x.iloc[:, s], data_x.iloc[:, s + 1 + i])[1, 0]))

参考