Convex-Hull(凸包)を用いたBoundingBoxの求め方
Convex-Hull(凸包アルゴリズム)は、各プロットが内在するような最小の図形である。
ここでは、2次元の散布図でConvex-Hullを求めて、次にBoundingBoxを求める。
散布図
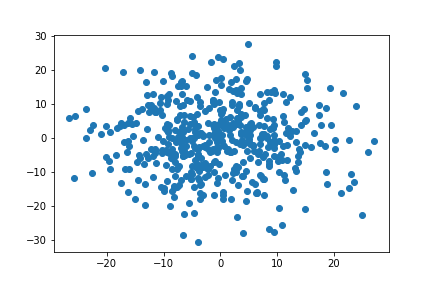
Convex-Hull
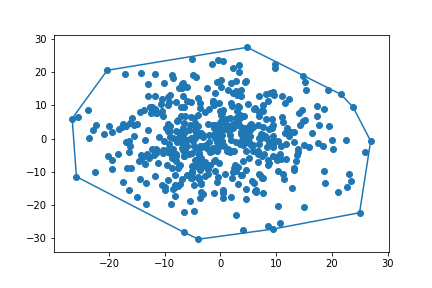
必要なPythonのライブラリ
import math import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.spatial import ConvexHull
Convex-Hullアルゴリズム
#元のプロット points = np.random.normal(0, 10, (500, 2)) plt.scatter(points[:, 0], points[:, 1]) plt.show() #Convex-Hull hull = ConvexHull(points) points = hull.points hull_points = points[hull.vertices] hp = np.vstack((hull_points, hull_points[0])) plt.plot(hp[:,0], hp[:,1]) plt.scatter(points[:,0], points[:,1]) plt.show()
散布図

Convex-Hull

Bounding-Box
points = np.random.normal(0, 10, (500, 2))
#Convex-Hull
hull = ConvexHull(points)
points = hull.points
hull_points = points[hull.vertices]
edge_angles = np.zeros(len(hull_points) - 1)
for i in range(len(edge_angles)):
edge_x = hull_points[i + 1, 0] - hull_points[i, 0]
edge_y = hull_points[i + 1, 1] - hull_points[i, 1]
edge_angles[i] = abs(math.atan2(edge_y, edge_x) % (math.pi / 2))
edge_angles = np.unique(edge_angles)
min_bbox = (0, sys.maxsize, 0, 0, 0, 0, 0)
for i in range(len(edge_angles)):
# create Rotation matrix
R = np.array([[math.cos(edge_angles[i]), math.cos(edge_angles[i] - (math.pi / 2))],
[math.cos(edge_angles[i] + (math.pi / 2)), math.cos(edge_angles[i])]])
rot_points = np.dot(R, hull_points.T)
# min max
min_x = np.nanmin(rot_points[0], axis=0)
max_x = np.nanmax(rot_points[0], axis=0)
min_y = np.nanmin(rot_points[1], axis=0)
max_y = np.nanmax(rot_points[1], axis=0)
# width heigh
width = max_x - min_x
height = max_y - min_y
area = width * height
# store the smallest
if (area < min_bbox[1]):
min_bbox = (edge_angles[i], area, width, height, min_x, max_x, min_y, max_y)
angle = min_bbox[0]
R = np.array([[math.cos(angle), math.cos(angle - (math.pi / 2))],
[math.cos(angle + (math.pi / 2)), math.cos(angle)]])
proj_points = np.dot(R, hull_points.T)
min_x = min_bbox[4]
max_x = min_bbox[5]
min_y = min_bbox[6]
max_y = min_bbox[7]
center_x = (min_x + max_x) / 2
center_y = (min_y + max_y) / 2
center_point = np.dot([center_x, center_y], R)
corner_points = np.zeros((4, 2))
corner_points[0] = np.dot([max_x, min_y], R)
corner_points[1] = np.dot([min_x, min_y], R)
corner_points[2] = np.dot([min_x, max_y], R)
corner_points[3] = np.dot([max_x, max_y], R)
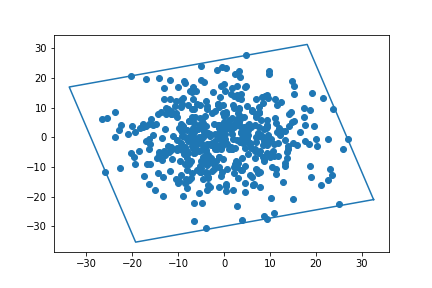
Gr = (corner_points[0,1] - corner_points[1, 1]) / (corner_points[0, 0] - corner_points[1, 0])
theta = math.atan(Gr)
R_coor = np.array([[ math.cos(theta), math.sin(theta) ],
[ -math.sin(theta), math.cos(theta)]])
a = np.dot(R_coor, points.T ).T
c = np.dot(R_coor, corner.T).T
plt.plot(c[:,0], c[:,1])
plt.scatter(a[:,0], a[:,1])
plt.show()
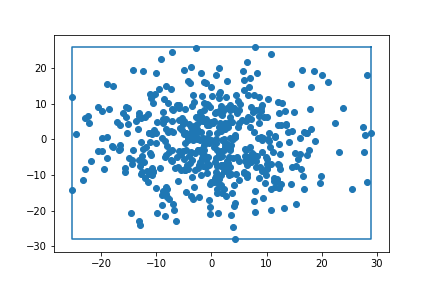
まとめ
散布図

Convex-Hull

Bounding-Box

Rotation Bounding-Box












