RV係数
RV係数は、2乗ピアソン相関係数の多変量一般化である。
\(0\leq RV \leq1\)の関係になっている。
$$
RV(X, Y) = \frac{\mathrm{Tr}(XX^{\mathrm{T}} YY^{\mathrm{T}})}{\{\mathrm{Tr}(X^2)\mathrm{Tr}(Y^2)\}^{\frac{1}{2}}}
$$
 画像処理
画像処理 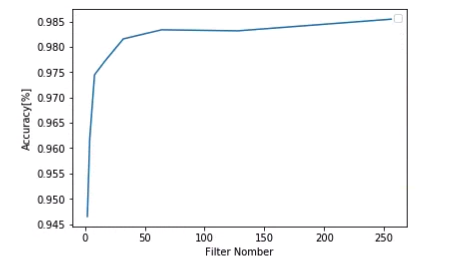 ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  C++
C++  fMRI Data Analysis
fMRI Data Analysis 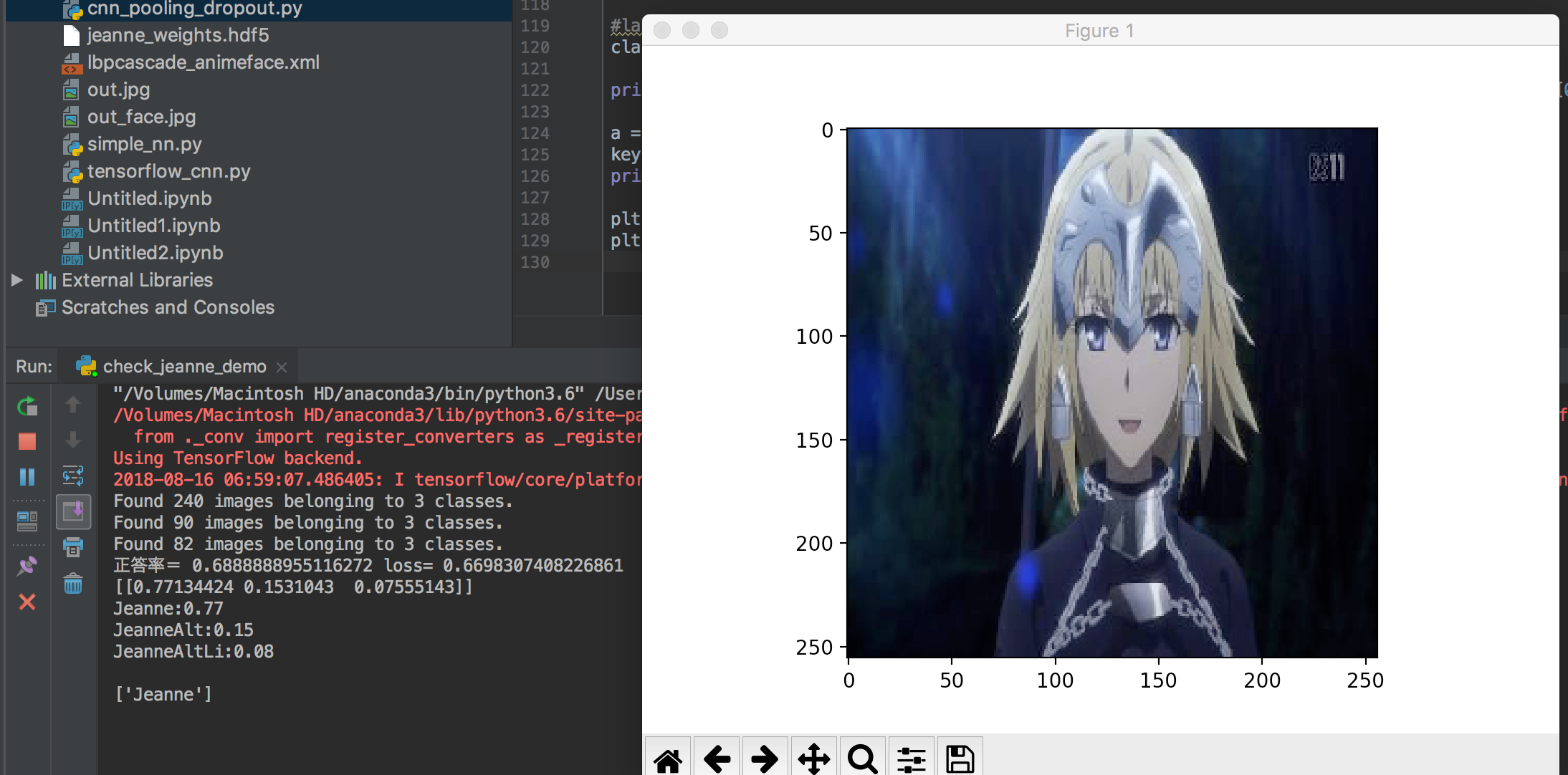 ディープラーニング
ディープラーニング  機械学習
機械学習  統計学
統計学  自然言語処理
自然言語処理 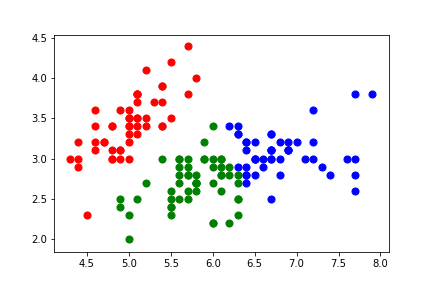 機械学習
機械学習  機械学習
機械学習  画像処理
画像処理  データサイエンス
データサイエンス  データサイエンス
データサイエンス  統計学
統計学  C++
C++ 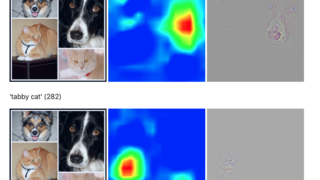 ディープラーニング
ディープラーニング  機械学習
機械学習  データサイエンス
データサイエンスRV係数は、2乗ピアソン相関係数の多変量一般化である。
\(0\leq RV \leq1\)の関係になっている。
$$
RV(X, Y) = \frac{\mathrm{Tr}(XX^{\mathrm{T}} YY^{\mathrm{T}})}{\{\mathrm{Tr}(X^2)\mathrm{Tr}(Y^2)\}^{\frac{1}{2}}}
$$