Pytorch入門-線形回帰モデル

線形回帰モデル

pythonで統計-単回帰

プログラム

%matplotlib inline
from matplotlib import pyplot as plt
import torch
from torch import nn, optim

w_true = torch.Tensor([1, 2, 3])
X = torch.cat([torch.ones(100,1), torch.randn(100, 2)], 1)
y = torch.mv(X, w_true) + torch.randn(100) * 0.5
w = torch.randn(3, requires_grad=True)


net = nn.Linear(in_features=3, out_features=1, bias=False)

optimizer = optim.SGD(net.parameters(), lr=0.1)

loss_fn = nn.MSELoss()

losses = []

for epoch in range(100):
    
    optimizer.zero_grad()
    
    y_pred = net(X)
    
    loss = loss_fn(y_pred.view_as(y), y)
    loss.backward()
    
    optimizer.step()
    losses.append(loss.item())
    print("epoch: %d , loss: %f" % (epoch+1, loss))
    if(epoch != 0):
        if(abs(losses[epoch-1] - losses[epoch]) < 0.00001):
            break
    

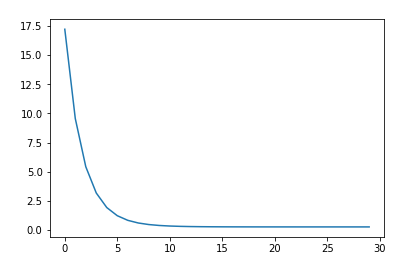
plt.plot(losses)
print(list(net.parameters()))

出力

epoch: 1 , loss: 17.221216
….
….
epoch: 30 , loss: 0.267617

tensor([[1.0030, 2.0557, 2.9886]], requires_grad=True)

参考

メモ

import torch

w_true = torch.Tensor([1, 2, 3])

X = torch.cat([torch.ones(100,1), torch.randn(100, 2)], 1)

y = torch.mv(X, w_true) + torch.randn(100) * 0.5

w = torch.randn(3, requires_grad=True)

gamma = 0.1

losses = []

for epoch in range(100):
    
    w.grad = None
    
    y_pred = torch.mv(X, w)
    
    loss = torch.mean((y - y_pred) ** 2)
    loss.backward()
    
    w.data = w.data -gamma * w.grad.data
    losses.append(loss.item())
    print("epoch: %d , loss: %f" % (epoch+1, loss))
    
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot(losses)

print(w.data)