主成分分析（PCA）sklearnとpython

主成分分析とは
主成分分析の流れ
プログラムでPCA
参考

主成分分析とは

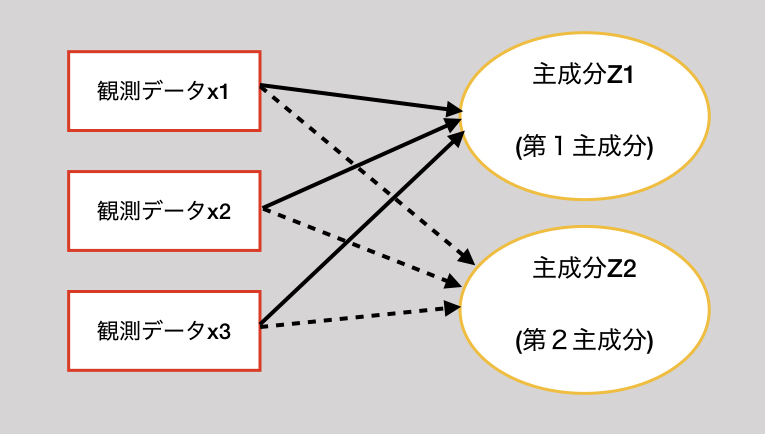
主成分分析は、観測変数から新しい変数（主成分という）を合成する分析手法です。

複数の観測変数を単純化し、標本が持っている情報をうまく要約します。

主成分は、観測データと直線との垂線の距離を最小になるような直線を引く。

（以下のようにも言える）
観測データの重心を通るように、最も散らばっている（分散の大きい）ところに直線を引く。

観測データの持つ情報量（主成分の固有値）が最大になるようなところに直線を引く。

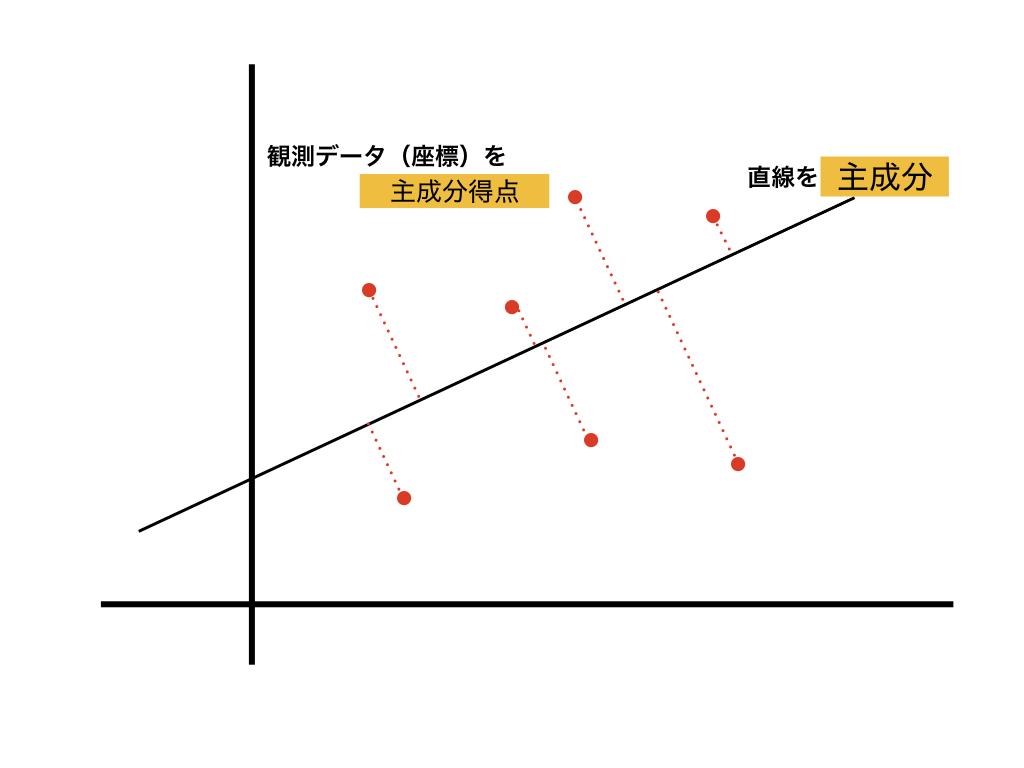
主成分分析では、一般的に第１主成分・第２主成分を使って、２次元のグラフで表す。

主成分分析の流れ

主成分と主成分得点を求める
分析結果の制度を確認する
分析結果を検討する

説明変数uとし、主成分Zとする。

$$Z = a_1u_1 + a_2u_2 + \cdots +a_pu_p$$
aは、Zへの影響度と解釈できる。

変数ごとに標準化
相関行列を求める

相関行列SSは、正方行列でもあり、対称行列でもある。

固有値、固有ベクトルを求める

$$SSx = \lambda x$$

$$\lambda = (\lambda_1, \cdots, \lambda_n)$$
$$u = (u_1, \cdots, u_n)$$

$\lambda$は、固有値
uは、固有ベクトルです。

第k主成分の寄与率
$$\frac{\lambda_k}{変数の個数}\times 100$$

プログラムでPCA

アルゴリズム

標準化
共分散行列
共分散行列の固有値を固有ベクトルを取得
次元数kを決める
上位k個の固有ベクトルの行列W
行列Wから、特徴ベクトルを取得する

skleanでPCA

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
 
cancer = load_breast_cancer()
train_X, val_X, train_y, val_y = train_test_split(cancer.data, cancer.target, test_size=0.3, random_state=0)
 
#PCA
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
std.fit(train_X)
 
std_train_X = std.transform(train_X)
std_val_X = std.transform(val_X)
 
from sklearn.decomposition import PCA
 
pca = PCA(n_components=2)
 
pca.fit(std_train_X)
 
pca_train_X = pca.transform(std_train_X)
pca_val_X = pca.transform(std_val_X)

numpyだけでPCA

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
 
cancer = load_breast_cancer()
train_X, val_X, train_y, val_y = train_test_split(cancer.data, cancer.target, test_size=0.3, random_state=0)
 
#標準化
std_value = train_X.std(axis=0)
mean_value = train_X.mean(axis=0)
s_train_X = (train_X - mean_value) / std_value
s_val_X = (val_X - mean_value) / std_value
 
#共分散行列
covs = np.cov(s_train_X.T)
 
#共分散行列の固有値と固有ベクトル
eigen_vals, eigen_vecs = np.linalg.eig(covs)
 
#次元数ncを決める
nc = 2
vals = eigen_vals[:nc]
vecs = eigen_vecs[:,:nc]
 
p_train_X = s_train_X.dot(vecs)
p_val_X = s_val_X.dot(vecs)

参考

[第2版]Python 機械学習プログラミング達人データサイエンティストによる理論と実践 (impress top gear)

機械学習のエッセンス -実装しながら学ぶPython,数学,アルゴリズム- (Machine Learning)