スパースモデリング-入門メモ-
「スパースモデリング」についてまとめていきます。
まず私は、数学が苦手なので、詳しい証明や導入式については省きます。
概念や使い方、特徴をまとめていきます。
参考書
岩波データサイエンス Vol.5
圧縮センシングMRIの基礎 (画像再構成シリーズ)
を参考に勉強しています。
スパースモデリングとは
スパースモデリングとは、与えられたデータに応じて、統計モデルの必要な部分を自動的に抽出する技術です。
重回帰分析では、多数の独立変数を扱うこともあります。
従来では、予測精度を上げるには、モデル選択や変数選択を行う必要があります。
これらの選択は、回帰係数等を求めた後に、統計指標(決定係数など)を算出し、検討する必要があります。
また、回帰係数を求める前に、多重共線性の有無を確かめる必要もあります。
多重共線性があると、正しく回帰係数が求められないことがあり、算出された回帰係数の信頼度が落ちてしまいます。
スパースモデリングでは、回帰係数の推定と同時に、重要な回帰係数を自動的に取り出すことが出来ます。
一方、重要でない回帰係数は、0に近づけられます。
L[n]ノルム
L[n]ノルムの定義式
*注意:nが1以上の時
$$ \Vert x \Vert_n = (\displaystyle \sum_{ i=1 }^{ N } |x_i|^n)^{\frac{1}{n}}$$
L0ノルム
L0ノルムは、非ゼロの値を持つベクトル成分の数のことである。
$$\Vert x \Vert_0 = \displaystyle \lim_{ p \to 0 } \sum_{ i=1 }^{ N } |x_i|^p $$
L1ノルム
L1ノルムは、ベクトル成分の値の絶対値の和のことである。
$$\Vert x \Vert_1 = \displaystyle \sum_{ i=1 }^{ N }|x_i|$$
L2ノルム
L2ノルムは、ベクトル成分の値の2乗和の平方根のことである。
$$\Vert x \Vert_2 = \sqrt {\displaystyle \sum_{ i=1 }^{ N }x_i^2} $$
ノルムの最小化
L0ノルム最小化
0でない要素が最も少ないものを求める。
$$ \hat{x}^{(0)} = arg\displaystyle \min_{ x } \Vert x \Vert_0 \ subj.to \ \mathrm{ y }=A \mathrm{ x }$$
組み合わせ爆発が避けられない
L1ノルム最小化
各要素の絶対値の和が最も小さい解を探す。
$$ \hat{x}^{(1)} = arg\displaystyle \min_{ x } \Vert x \Vert_1 \ subj.to \ \mathrm{ y }=A \mathrm{ x }$$
L0ノルム最小化として得られる解と多くの場合一致する。
L2ノルム最小化
ベクトル成分の値の2乗和の平方根がもっとも小さい解を探す。
$$ \hat{x}^{(2)} = arg\displaystyle \min_{ x } \Vert x \Vert_2 \ subj.to \ \mathrm{ y }=A \mathrm{ x }$$
スパース解が得られるとは限らない。
概念図
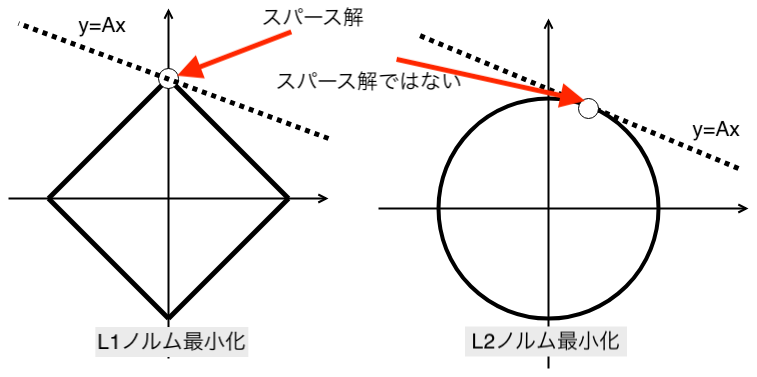
(N=2, K=1, M=1)の場合
図の太線で囲まれた面積が、L1または、L2ノルムである。
縦軸と横軸はベクトルx1,x2で、点線はy=Axの条件を表す。白丸は、推定値(xの解)を表す。
L2ノルムは、スパース解が得られないことがある例である。
スパース回帰
リッジ回帰は、変数選択を助ける回帰方法である。
従来の重回帰
重回帰では、最小二乗法を用いる
従来では、ある項を取り入れない場合は、その項の変数を削除してしまう。
$$ \beta_1x_1 + \beta_2x_2$$
上記の式で、β2が要らないと判断した場合は、その変数x2を削除する。言い換えると、x1だけを採用することになります。
Pythonで重回帰

リッジ回帰
リッジ回帰では、最小二乗法に「罰則項」を付け加える。
L2正則化を用いて、推定する。
$$min \displaystyle \sum_{ i }^{ } (y_i – \displaystyle \sum_{ j }^{ } \beta_jx_i^{j})^2 + \lambda\displaystyle \sum_{ j }^{ } \Vert \beta \Vert_2^2$$
回帰係数を、罰則項を付加して推定することから、罰則つき推定と言われます。
λは、自分で決める必要があります。
リッジ回帰は、ぴったり0に縮小することが出来ないことに注意が必要です。
- λを大きくすると「0に近い」と推定されるパラメータの数が多くなる!
- λを小さくすると「0に近い」と推定されるパラメータの数が少なくなる!
Python

Lasso回帰
Lasso回帰は、スパース性を用いたリッジ回帰である。
L1正則化を用いて、推定する。
$$min \displaystyle \sum_{ i }^{ } (y_i – \displaystyle \sum_{ j }^{ } \beta_jx_i^{j})^2 + \lambda\displaystyle \sum_{ j }^{ } \Vert \beta \Vert_1$$
罰則項が、回帰係数の絶対値に変わっただけである。
これは、Lasso(Least Absolute Shrinkage and Selection Operator)と呼ばれるスパース性を利用した推定方法である。
- λを大きくすると 「ゼロ」 と推定されるパラメータの数が多くなる!
- λを小さくすると 「ゼロ」 と推定されるパラメータの数が少なくなる!
Python

elastic net
説明変数の中に非常に相関の高いものがるときにはそれらの間で推定が不安定になることが知られている。
これは、多重共線性として知られている。
この多重共線性が生じる場合、正則化項として、ridge回帰とlasso回帰で用いる正則化項の両方を使う方法をelastic netという。
L1ノルムの割合を(1-α)とし、L2ノルムの割合をαと設定する。
$$min \left[ \Vert y – \displaystyle \sum_{ j }^{ } \beta_jx_i^{j} \Vert_2^2 + \lambda( (1-\alpha)\Vert \beta \Vert_1 + \alpha \Vert \beta \Vert_2^2 ) \right]$$
Python