仮説検定をPythonで解く

この記事の目的

前回の仮説検定について、実際に問題を解くこと。

仮説検定

betashort-lab.com

2018.06.19

必要なライブラリ

numpyとscipyのstatsをインポートします。

import numpy as np
import scipy.stats as stats

母分散が既知の時、母平均の検定

前提条件-パラメータ-

母分散は、1.44
母平均（帰無仮説）は、50と設定
標本の個数は、9
標本平均は、49.9

sigma2 = 1.44 
mu_s = 50

n = 9
x_bar = 49.4

No1 帰無仮説

$$\mu = 50$$

No2 対立仮説

$$mu \neq 50$$

==>両側検定になる

統計量を計算する

$$ 統計量 Z = \displaystyle \frac{ \bar{ X } – \mu }{ \sqrt{ \frac{ \sigma^2 }{ n }} } $$

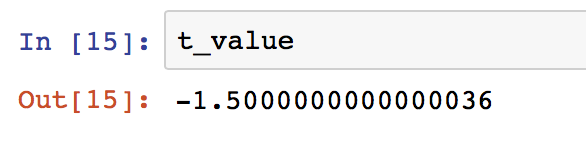
t_value = (x_bar-mu_s)/ np.sqrt(sigma2 / n)

No4 有意水準にもとづいて、棄却域を求める

$$ \displaystyle \frac{ \bar{ X } – \mu }{ \sqrt{ \frac{ \sigma^2 }{ n }} } \leq -Z_{ \frac{\alpha}{2}} $$
$$ Z_{ \frac{\alpha}{2}} \leq \displaystyle \frac{ \bar{ X } – \mu }{ \sqrt{ \frac{ \sigma^2 }{ n }} } $$

有意水準を0.05と設定する。

alpha_r = 0.05

t = abs(stats.norm.ppf(alpha_r/2))

棄却域は、
$$ t_value < -t || t < t_value$$

帰無仮説を棄却するか判断

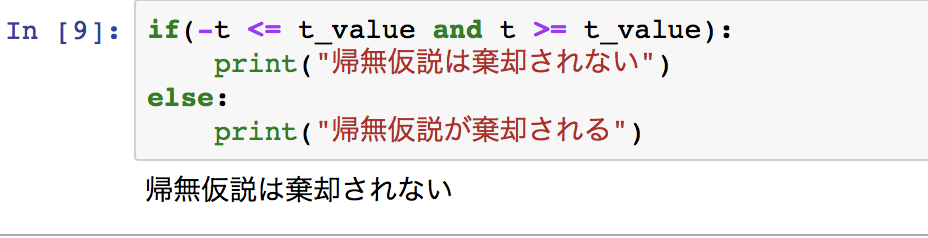
if(-t <= t_value and t >= t_value):
    print("帰無仮説は棄却されない")
else:
    print("帰無仮説が棄却される")

母分散が未知の時、母平均の検定

前提条件-パラメータ-

x = [9.8,10.3,11.9,8.7,9.5,10.2,10.9,8.2,9.4,10.5]
n = len(x)
x_bar = np.mean(x)
s2_x = np.var(x, ddof=1)
s_x = np.std(x, ddof=1)

No1 帰無仮説

$$\mu = 10$$

No2 対立仮説

$$\mu < 10$$ ==>片側検定

統計量を計算する

$$ 統計量 T = \displaystyle \frac{ \bar{ X } – \mu }{ \sqrt{ \frac{ S^2 }{ n }} } $$

mu =10 #帰無仮説
t_value = (x_bar - mu) / (s_x / np.sqrt(n))

No4 有意水準にもとづいて、棄却域を求める

$$ \displaystyle \frac{ \bar{ X } – \mu }{ \sqrt{ \frac{ \sigma^2 }{ n }} } \leq -t_{ \alpha} $$

有意水準を0.05と設定する。

alpha_r = 0.05

t = abs(stats.t.ppf(alpha_r, n-1))

棄却域は、
$$ t_value < -t $$

帰無仮説を棄却するか判断

if( t_value < -t):
    print("帰無仮説は棄却される\n")
else:
    print("帰無仮説は棄却されない\n")

母分散の検定

前提条件-パラメータ-

x = [9.8,10.3,11.9,8.7,9.5,10.2,10.9,8.2,9.4,10.5]
n = len(x)
x_bar = np.mean(x)
s2_x = np.var(x, ddof=1)
s_x = np.std(x, ddof=1)

No1 帰無仮説

$$\sigma^2 = 0.5$$

No2 対立仮説

$$\sigma^2 \neq 0.5$$
==>両側検定

統計量を計算する

$$ 統計量 \chi^2 = \displaystyle \frac{ S^2 }{ \frac{ \sigma^2 }{ n-1 } } $$

sigma2 = 0.5 #帰無仮説
chi_2_value = (n-1)*s2_x/sigma2

No4 有意水準にもとづいて、棄却域を求める

$$ \chi^2_{(\frac{\alpha}{2}, m)} \leq \displaystyle \frac{ S^2 }{ \frac{ \sigma^2 }{ n-1 } } \leq \chi^2_{(1-\frac{\alpha}{2}, m)} $$

有意水準を0.05と設定する。

alpha_r = 0.05
chi_2_1 = stats.chi2.ppf(alpha_r/2, n-1)
chi_2_2 = stats.chi2.ppf(1-alpha_r/2, n-1)

棄却域は、
chi_2_value < chi_2_2 and chi_2_1 < chi_2_value

帰無仮説を棄却するか判断

if (chi_2_2<chi_2_value and chi_2_value < chi_2_1):
    print("帰無仮説は棄却されない")
else:
    print("帰無仮説は棄却される")

参考書