多重共線性
説明変数間の関係に、線形従属の関係が成り立つとき、これを「完全な多重共線性がある」という。
説明変数間に高い関連性がある時、多重共線性があるという。
完全な多重共線性でなくても、高い関連性が認められたときは、多重共線性に配慮しなければならない。
多重共線性がある場合、回帰係数を正しく計算できなくなります。
多重共線性がある場合、推定偏回帰係数の分散が大きくなる。
一般的にVIF統計量が10以上であれば、多重共線性が存在している可能性があります。
なので、VIFが10以上になるかどうかチェックします。
VIFとは
VIFは、Variance Inflation Factorの略です。
日本語でいうと、分散拡大要因です。
統計学における分散拡大係数(variance inflation factor, VIF) とは、最小二乗回帰分析における多重共線性の深刻さを定量化する。推定された回帰係数の分散(推定値の標準偏差の平方)が、多重共線性のためにどれだけ増加したかを測る指標を提供する。
分散拡大係数-Wikipedia
VIFの求め方
VIFの求め方は、何通りかあります。
VIFの求め方は、2つ目で紹介する「決定係数を使ったVIFの求め方」が一般的です。
1つ目の「説明変数間の相関係数を使ったVIFの求め方」では、各説明変数間の相関について調べています。
組み合わせが
$$\begin{eqnarray}{}_n \mathrm{ C }_k = \frac{ n! }{ k! ( n – k )! }\end{eqnarray}$$
と、増加するため、説明変数間のグルーピング(変数の選択)が、かなり複雑になります。
2つは、決定係数を使ったVIFの求め方
説明変数間の相関係数を使ったVIF
$$VIF=\frac{ 1 }{ 1 – r^2 }$$
$$rは、相関係数です。r = \frac{ \sigma_{x1x2} }{ \sigma_{x1} \sigma_{x2} }$$
$$\sigma_{x1x2}は、共分散$$
$$\sigma_{x1}と\sigma_{x2}は、標準偏差(分散の平方根)です。$$
計算例
今回は、多重共線性とVIF統計量で説明変数間での相関を調べるのデータを使ってVIF統計量を計算します。
使用するデータは、変数が3つです。
変数をそれぞれx1,x2,x3とします。
比較する組み合わせは、下図のように3通りです。
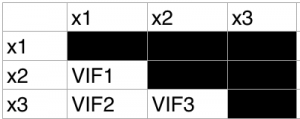
これは、高校数学でやった組み合わせで計算します。
nは、変数の数です。kは、2となります。
$$\begin{eqnarray}{}_n \mathrm{ C }_k = \frac{ n! }{ k! ( n – k )! }\end{eqnarray}$$
Excel(Numbers)で相関係数VIF
相関係数を求めるには、CORREL(列1,列2)を使います。
Numbersについても同じ関数です。
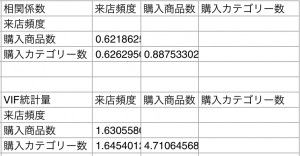
C++で相関係数VIF
C++のプログラムは、以下のリンクにあります。
練習問題として、
多重共線性とVIF統計量で説明変数間での相関を調べる
の問題を解いています。
Pythonで相関係数VIF
Pythonのコードは以下のリンクにあります。
決定係数を使ったVIF
以下の計算アルゴリズムは、分散拡大係数-wikiを参照しました。
分かりやすいので、ぜひ参照してほしいです。
以下の k 個の独立変数を持った線形モデル(linear model)を考える。
Y = β0 + β1 X1 + β2 X 2 + … + βk Xk + ε
ステップ1
最初に、Xiを目的変数とし、他の変数を説明変数とした最小二乗回帰を行う。 i = 1 であれば、以下のような等式となる。
$${\displaystyle X_{1}=\alpha _{2}X_{2}+\alpha _{3}X_{3}+\cdots +\alpha _{k}X_{k}+c_{0}+e}$$
ここで、c0 は定数であり、e は誤差である。
ステップ2
次式により、 $${\displaystyle {\hat {\beta }}_{i}}$$に対する VIF ファクターを計算する。
$${\displaystyle \mathrm {VIF_{i}} ={\frac {1}{1-R_{i}^{2}}}}$$
ここで、R2i はステップ1における回帰の決定係数である。
ステップ3
$${\displaystyle VIF ({\hat {\beta }}_{i})}$$の大きさを考慮し、多重共線性の程度を分析する。
決定係数の求め方
決定係数の求め方は、決定係数-wikiを参照しました。
$${\displaystyle R^{2}\equiv 1-{\sum _{i}(y_{i}-f_{i})^{2} \over \sum _{i}(y_{i}-{\bar {y}})^{2}}}$$
説明変数が多い場合の自由度調整済みの決定係数
$${\displaystyle R’^{2}\equiv 1-{{\sum _{i}(y_{i}-f_{i})^{2}/(N-p-1)} \over {\sum _{i}(y_{i}-{\bar {y}})^{2}/(N-1)}}}$$
Pythonの場合
PythonでVIFを確認するには、ライブラリを使うと便利です。
予測と分析における多重共線性
予測と分析では、多重共線性の捉え方が違うのではないかと思っています。
(論理的な・理論的な話ではありませんが)
多重共線性が認められるデータを使って、重回帰分析をしたとします。
この場合、経験として、
- 多重共線性が認められたデータのまま重回帰分析を行ったときの予測誤差
- 多重共線性を除去したデータで重回帰分析を行ったときの予測誤差
では、多重共線性が認められたデータのまま重回帰分析を行ったときの予測誤差の方が、小さい印象です。
予測の場合では、予測誤差が小さい方が良いので、「多重共線性が認められたデータ」でも良いのではないかと思います。
ただし、オーバーフィッティング気味という話を聞いた気がします。。。
分析の場合は、推定偏回帰係数の検定(t検定やF検定など)をする必要があるので、多重共線性が認められたデータを使うのは問題があると思います。
また、機械学習の参考書では、多重共線性の話が出てくるものが少ない印象です。
機械学習では、予測に重きを置くというイメージです。
一方、統計学の参考書では、多重共線性の話が出てきます。
(多重共線性までの話が出てくるが、詳しく書いている本は少なめな印象)
統計学は、分析に重きを置くというイメージです。
このように、予測と分析では、多重共線性における捉え方が違うのかなと思っています。