重回帰分析とは
回帰係数が2つ以上で従属変数も2つ以上
下の式で表せる回帰を重回帰と言う。
$$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2+\cdots + \beta_n x_n$$
計算式
説明変数の個数をn、データ数をmとする。
Xとyを以下のようにする。
\begin{eqnarray}
\boldsymbol{X}= \left(
\begin{array}{cccc}
1 & a_{ 11 } & a_{ 21 } & \ldots & a_{ n1 } \\
1 & a_{ 12 } & a_{ 22 } & \ldots & a_{ n2 } \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & a_{ 1m } & a_{ 2m } & \ldots & a_{ nm }
\end{array}
\right)
\end{eqnarray}
\begin{eqnarray}
\boldsymbol{y}=\left(
\begin{array}{c}
y_1 \\
y_2 \\
\vdots \\
y_m
\end{array}
\right)
\end{eqnarray}
推定値\(\hat{\boldsymbol{\beta}}\)は、以下のように計算することができる。
$$\huge{\hat{\boldsymbol{\beta}} = (\boldsymbol{X}^t \boldsymbol{X})^{-1} \boldsymbol{X}^t \boldsymbol{y}}$$
なお、推定値\(\hat{\boldsymbol{\beta}}\)は、以下のベクトル列と算出される。
\begin{eqnarray}
\hat{\boldsymbol{\beta}}=\left(
\begin{array}{c}
\beta_0 \\
\beta_1 \\
\vdots \\
\beta_n
\end{array}
\right)
\end{eqnarray}
標準偏回帰係数
全ての変数を標準化して、重回帰分析を行う。
$$\frac{x_i-\bar{x_i}}{ S_{x_i} }$$
Sは、標準偏差です。
その時の偏回帰係数を、標準偏回帰係数と呼ぶ。
決定係数
決定係数は、データに対する、推定された回帰式の当てはまりの良さを表します。
重回帰分析では、自由度調整済み決定係数を使います。
pは、説明変数の数です。
$${\displaystyle R’^{2}\equiv 1-{{\sum _{i}(y_{i}-f_{i})^{2}/(N-p-1)} \over {\sum _{i}(y_{i}-{\bar {y}})^{2}/(N-1)}}}$$
t検定
偏回帰係数が0と有意に異なっているかどうかを検定する。
帰無仮説は、$$\beta = 0$$となる。
*回帰分析のt値についてまとめました。合わせて、参照してください。
回帰分析のt値について
F検定
重回帰分析で、回帰式そのものが統計的に意味があるかどうか知りたい場合
全ての偏回帰係数が0であるという帰無仮説の下でF検定を行う。
多重共線性(マルチコ)
説明変数間に高い関連性がある時、多重共線性があるという。
多重共線性がある場合、回帰係数を正しく計算できなくなります。
$$\hat{\boldsymbol{\beta}} = (\boldsymbol{X}^t \boldsymbol{X})^{-1} \boldsymbol{X}^t \boldsymbol{y}$$
より、逆行列を求める
$$(\boldsymbol{X}^t \boldsymbol{X})^{-1}$$
が正則行列でない(特異行列)場合、計算できなくなります。
完全な多重共線性の場合、列・行ベクトルの線型独立性が成り立たない。
逆行列の求め方-with-python
特殊な行列をまとめる逆行列・正則行列な
多重共線性については、下のリンクを参照してください。
多重共線性とVIF統計量の求め方
参考
重回帰分析をPythonで実装
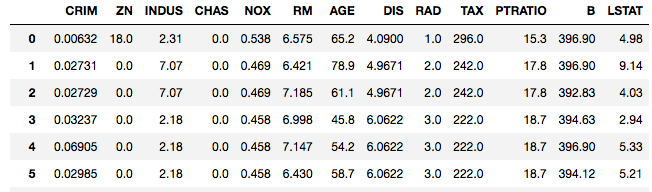
データには、ボストンデータを使います。
Xの変数は、13個の重回帰式になります。
最小2乗法による重回帰を実行していきましょう。
scikit-learnで重回帰分析
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
# サンプルデータを用意
dataset = load_boston()
# 説明変数データを取得
data_x = pd.DataFrame(dataset.data, columns=dataset.feature_names)
#被説明変数データを取得
data_y = pd.DataFrame(dataset.target, columns=['target'])
#データの
print("説明変数行列のサイズ:{}".format(data_x.shape[1]))
print("被説明変数のサイズ:{}".format(data_y.shape))
print("説明変数の変数の個数:{}".format(data_x.shape[1]))
coef_n = data_x.shape[1]
decimal_p = 2
#最小2乗法による偏係数
OLS = LinearRegression().fit(data_x, data_y)
print(OLS.coef_.round(decimal_p))
結果
[[-1.07170557e-01 4.63952195e-02 2.08602395e-02 2.68856140e+00
-1.77957587e+01 3.80475246e+00 7.51061703e-04 -1.47575880e+00
3.05655038e-01 -1.23293463e-02 -9.53463555e-01 9.39251272e-03
-5.25466633e-01]]
statsmodelsで重回帰分析
statsmodelsでは、デフォルトで切片がない。
sm.OLS(data_y, sm.add_constant(data_X))
上のように、sm.add_constant()を用いることで、切片があり皆既になる。
import pandas as pd import matplotlib.pyplot as plt import numpy as np from sklearn.linear_model import LinearRegression from sklearn.datasets import load_boston # サンプルデータを用意 dataset = load_boston() # 説明変数データを取得 data_X = pd.DataFrame(dataset.data, columns=dataset.feature_names) #被説明変数データを取得 data_y = pd.DataFrame(dataset.target, columns=['target']) #statsmodelsをインポート import statsmodels.api as sm model = sm.OLS(data_y, sm.add_constant(data_X)) result = model.fit() result.summary()
結果
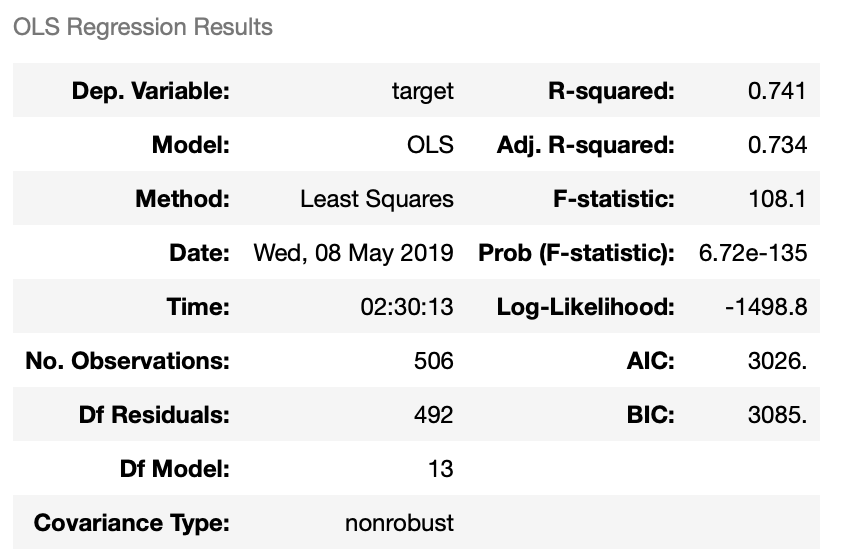
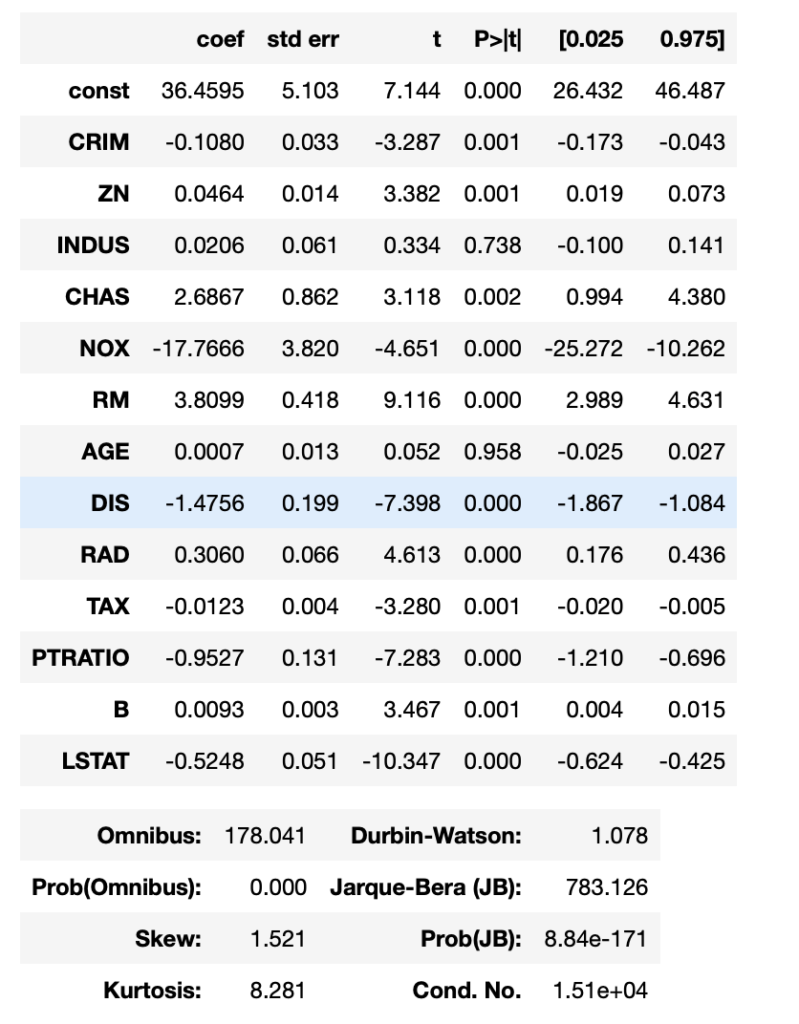
numpyで重回帰分析
import pandas as pd import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import load_boston # サンプルデータを用意 dataset = load_boston() # 説明変数データを取得 data_x = pd.DataFrame(dataset.data, columns=dataset.feature_names) #被説明変数データを取得 data_y = pd.DataFrame(dataset.target, columns=['target']) seg = np.ones((506, 1)) X = np.c_[seg, data_x] X_t = X.T beta_hat = np.dot(np.dot(np.linalg.inv(np.dot(X_t, X)), X_t), data_y) print(beta_hat.T)
結果
[[-1.07170557e-01 4.63952195e-02 2.08602395e-02 2.68856140e+00
-1.77957587e+01 3.80475246e+00 7.51061703e-04 -1.47575880e+00
3.05655038e-01 -1.23293463e-02 -9.53463555e-01 9.39251272e-03
-5.25466633e-01]]