 C++
C++
[C++]vector合成&削除メモ
 C++
C++  fMRI Data Analysis
fMRI Data Analysis  fMRI Data Analysis
fMRI Data Analysis  機械学習
機械学習  ディープラーニング
ディープラーニング  統計学
統計学  画像処理
画像処理  データサイエンス
データサイエンス  機械学習
機械学習  画像処理
画像処理 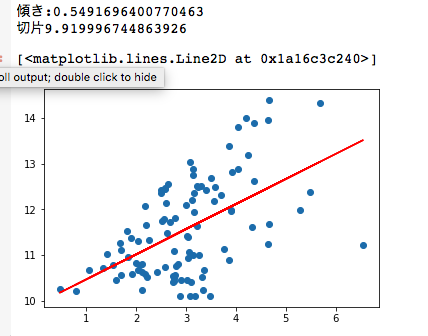 Python
Python  データサイエンス
データサイエンス 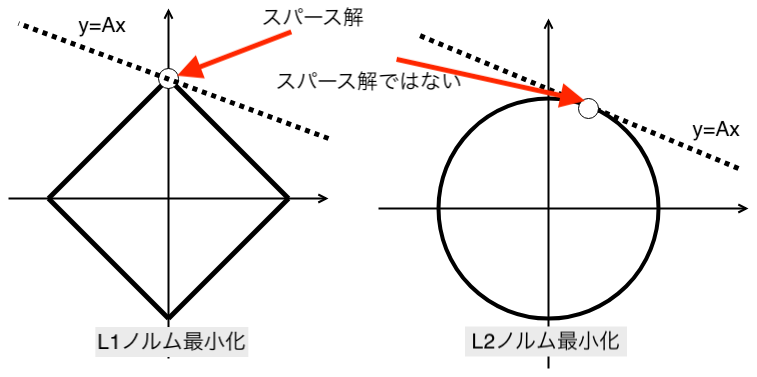 統計学
統計学  データサイエンス
データサイエンス  C++
C++  機械学習
機械学習  画像処理
画像処理  ディープラーニング
ディープラーニング  機械学習
機械学習 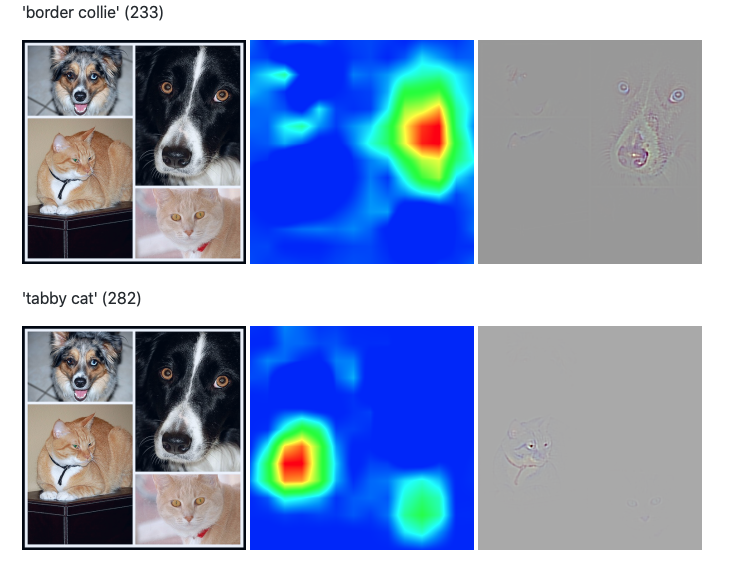 ディープラーニング
ディープラーニング  データサイエンス
データサイエンス  データサイエンス
データサイエンス  機械学習
機械学習  ディープラーニング
ディープラーニング  データサイエンス
データサイエンス  ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  ディープラーニング
ディープラーニング  機械学習
機械学習  Python
Python  ディープラーニング
ディープラーニング  統計学
統計学  機械学習
機械学習  統計学
統計学  統計学
統計学  統計学
統計学  データサイエンス
データサイエンス  データサイエンス
データサイエンス  機械学習
機械学習